Gyromagnetic Ratio (γ)

What is the gyromagnetic ratio (γ)?  

The concept of spin (I or S) was introduced in a prior Q&A to denote the intrinsic angular momentum of atomic and subatomic particles like electrons, protons, and whole nuclei. In an earlier Q&A on basic magnetism, we also defined the concept of a magnetic moment (μ), a vector-like quantity useful to describe how a small magnetic dipole (or current loop) interacts with an external magnetic field. There is no doubt that spin and magnetism of particles are closely related, but exactly how?

The answer lies in a fundamental symmetry theorem from quantum mechanics.  Specifically, spin and a particular form of the magnetic moment are collinear and directly proportional to one another connected by a constant (γ) called the gyromagnetic ratio:

μ = γ I      (for nucleus)
 μ = γ S     (for electron)

The value of the gyromagnetic ratio (γ) varies by atomic species. The units of γ are typically given in the form of [frequency]  ÷ [magnetic field strength], such as (radians/sec)/gauss or MHz/tesla. The reason for these units will become apparent in subsequent Q&As where the famous Larmor equation relating resonance frequency to field strength will be discussed.

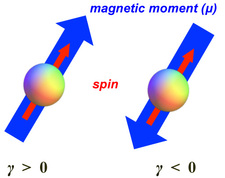
Most atomic nuclei have positive gyromagnetic ratios, but a few nuclei and the electron have negative values (γ < 0). When γ > 0 the spin and magnetic moment point in the same direction; for negative γ they are still collinear but lie in opposite directions. Two particles with positive and negative γ's precess in opposite directions.

Advanced Discussion (show/hide)»

For simplicity with the general readership, note that in the description above I have treated I, S, and μ as simple vectors, whereas they are actually quantum mechanical operators.

The collinearity and proportionality between spin angular momentum (I or S) and magnetic moment (μ) is a consequence of a fundamental symmetry relation in quantum mechanics (the Wigner-Eckart Theorem). As a direct result of this theorem, the expectation value of any vector operator of a system is equal to the projection onto its total angular momentum. For a more complete discussion/derivation see the following reference:

Berkeley Dept of Physics, Physics 221A. Lecture Notes: Irreducible Tensor Operators and the Wigner-Eckart Theorem (pdf), 2010.

---

References
      "Gyromagnetic Ratio", Wikipedia. The Free Encyclopedia.

---

Related Questions
     What is a magnetic moment? Is it the same as a magnetic dipole?
     What is spin?
     Who was Larmor and how did he discover his famous frequency?  
 

---

←  Previous Question

Next Question  →

↑ Complete List of Questions ↑